Rotor efficiency analysis
Posted by

 Dusan
–
Dusan
–
 Dusan
–
Dusan
–

Introduction
I always suspected the large rotor or propeller cannot have high efficiency at higher speeds and the general rule of thumb for propellers "larger is always better" cannot be true in all conditions, and above a certain speed the reverse is true. The efficiency analysis presented is based on the simple momentum theory, with added effects of flow viscosity over the blades, extracted from airfoil data.
Efficiency based on momentum theory
The momentum theory predicts that the efficiency depends on the free air velocity, the aircraft speed and the ultimate slip stream velocity
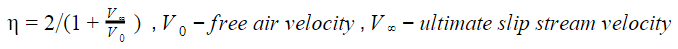
The thrust is
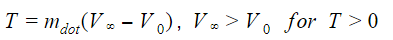
In order to maximize the efficiency, the overall induced velocity
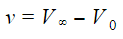
should be as small as possible. Reducing the induced velocity, the thrust reduces as well, so to develop the same thrust, the mass flow
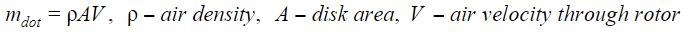
should be made larger, and the single way to do that is to increase the disk area A, as the air density is pretty much constant and from the moment theory for open rotors
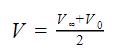
All this reasoning is especially valid at slow speed, and along the same lines is the cause that helicopters have large rotors.
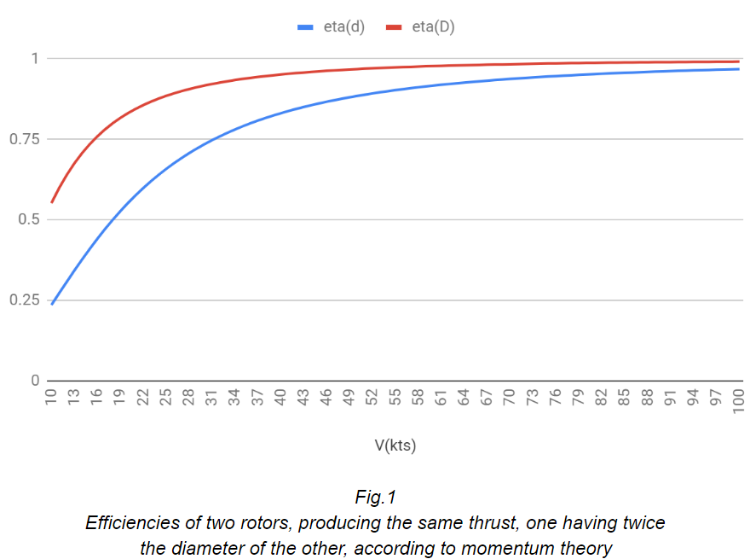
As speed increases, mass flow also increases, so the diameter is having less “weight” on the efficiency. This is also shown in the above plot, representing the efficiencies of two rotors, producing the same thrust, one having twice the diameter of the other. Let's call these rotors the L-rotor for the larger diameter rotor and S-rotor for the smaller one. At slow speed, the L-rotor efficiency, "eta(D)", is much higher than the S-rotor efficiency, "eta(d)", as expected. At high speed, the efficiency of both rotors are close to each other, so the diameter size is less important.
From the plot above, it seems that at very high speeds the efficiency approaches one, but let’s not forget, the momentum theory is valid only for inviscid flow, so the viscosity effects are not considered.
Adjusting efficiency for friction drag effects
Let’s add the effects of viscosity, especially friction drag. The friction drag is
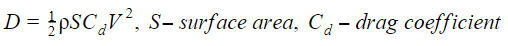
Considering similar blade geometry for both rotors, the L-rotor is having 4 times as much blade surface area. Looking at airfoil data for the NACA 0012 airfoil, a typical all-purpose airfoil, and comparing for Re 1,000,000 and 500,000 , L/D is 75.6 and respectively 61.7
This means that for the same lift, the drag coefficient is increased by 22.5% for the smaller Reynolds number. Using the previously mentioned drag coefficients, the drag of the L-rotor is still 3.26 times larger than the drag of the S-rotor at any speed, even that the L-rotor has a lower drag coefficient. Assuming blades are having constant tip speed, the drag for each rotor is constant. Plotting all this information, we’re getting this nice graph:
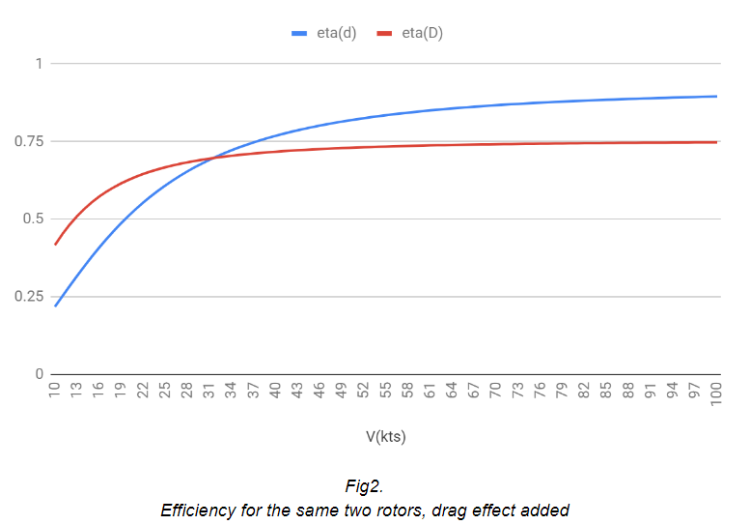
At slow speed the efficiency of the L-rotor is larger. As the speed is increased, the rotors diameter have less influence on the efficiency, drag “takes over” driving efficiency to drop, faster for the L-rotor as its drag is larger.
Now, some people might think: “If a smaller rotors is having less drag at higher speeds, would not a quad-copter having smaller rotors be more efficient than a helicopter at higher speeds?” This reasoning is false; the only reason the drag of the S-rotor is smaller is that its blade surface area is 4 times less than the L-rotor. A quad-copter having 4 rotors, the total drag is 4 times larger, moreover the blades are having a larger drag coefficient caused by Reynolds number difference. Taking all this into account, the total drag of the blades for a quad-copter is 22.5% higher vs a helicopter, assuming same disk loading (the blade area is equal for similar geometry rotors).
Conclusion
The rotor for a VTOL vehicle has conflicting requirements: In hover and slow speed the rotor diameter should be as large as possible, to reduce disk loading and implicitly the power required for hover. At high speed, the rotor diameter should be smaller to reduce its drag. This was recognized early by NASA and other corporations, a representative study in the field is "Dynamic Model Wind Tunnel Tests of a Variable-Diameter, Telescoping-Blade Rotor System (TRAC Rotor), Evan A. Fradenburgh, Robert J Murrill, Edmond F Kiely" link: https://apps.dtic.mil/dtic/tr/fulltext/u2/771037.pdf Another document having a nice explanation of why the efficiency of the tiltrotor is low in cruise mode, and why a variable-diameter rotor is beneficial is here: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19970005490.pdf
I always suspected the large rotor or propeller cannot have high efficiency at higher speeds and the general rule of thumb for propellers "larger is always better" cannot be true in all conditions, and above a certain speed the reverse is true. The efficiency analysis presented is based on the simple momentum theory, with added effects of flow viscosity over the blades, extracted from airfoil data.
Efficiency based on momentum theory
The momentum theory predicts that the efficiency depends on the free air velocity, the aircraft speed and the ultimate slip stream velocity
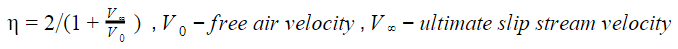
The thrust is
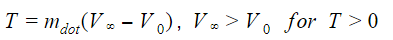
In order to maximize the efficiency, the overall induced velocity
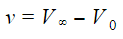
should be as small as possible. Reducing the induced velocity, the thrust reduces as well, so to develop the same thrust, the mass flow
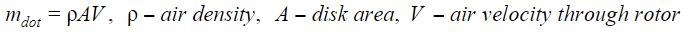
should be made larger, and the single way to do that is to increase the disk area A, as the air density is pretty much constant and from the moment theory for open rotors
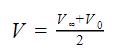
All this reasoning is especially valid at slow speed, and along the same lines is the cause that helicopters have large rotors.

As speed increases, mass flow also increases, so the diameter is having less “weight” on the efficiency. This is also shown in the above plot, representing the efficiencies of two rotors, producing the same thrust, one having twice the diameter of the other. Let's call these rotors the L-rotor for the larger diameter rotor and S-rotor for the smaller one. At slow speed, the L-rotor efficiency, "eta(D)", is much higher than the S-rotor efficiency, "eta(d)", as expected. At high speed, the efficiency of both rotors are close to each other, so the diameter size is less important.
From the plot above, it seems that at very high speeds the efficiency approaches one, but let’s not forget, the momentum theory is valid only for inviscid flow, so the viscosity effects are not considered.
Adjusting efficiency for friction drag effects
Let’s add the effects of viscosity, especially friction drag. The friction drag is
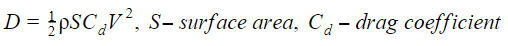
Considering similar blade geometry for both rotors, the L-rotor is having 4 times as much blade surface area. Looking at airfoil data for the NACA 0012 airfoil, a typical all-purpose airfoil, and comparing for Re 1,000,000 and 500,000 , L/D is 75.6 and respectively 61.7
This means that for the same lift, the drag coefficient is increased by 22.5% for the smaller Reynolds number. Using the previously mentioned drag coefficients, the drag of the L-rotor is still 3.26 times larger than the drag of the S-rotor at any speed, even that the L-rotor has a lower drag coefficient. Assuming blades are having constant tip speed, the drag for each rotor is constant. Plotting all this information, we’re getting this nice graph:

At slow speed the efficiency of the L-rotor is larger. As the speed is increased, the rotors diameter have less influence on the efficiency, drag “takes over” driving efficiency to drop, faster for the L-rotor as its drag is larger.
Now, some people might think: “If a smaller rotors is having less drag at higher speeds, would not a quad-copter having smaller rotors be more efficient than a helicopter at higher speeds?” This reasoning is false; the only reason the drag of the S-rotor is smaller is that its blade surface area is 4 times less than the L-rotor. A quad-copter having 4 rotors, the total drag is 4 times larger, moreover the blades are having a larger drag coefficient caused by Reynolds number difference. Taking all this into account, the total drag of the blades for a quad-copter is 22.5% higher vs a helicopter, assuming same disk loading (the blade area is equal for similar geometry rotors).
Conclusion
The rotor for a VTOL vehicle has conflicting requirements: In hover and slow speed the rotor diameter should be as large as possible, to reduce disk loading and implicitly the power required for hover. At high speed, the rotor diameter should be smaller to reduce its drag. This was recognized early by NASA and other corporations, a representative study in the field is "Dynamic Model Wind Tunnel Tests of a Variable-Diameter, Telescoping-Blade Rotor System (TRAC Rotor), Evan A. Fradenburgh, Robert J Murrill, Edmond F Kiely" link: https://apps.dtic.mil/dtic/tr/fulltext/u2/771037.pdf Another document having a nice explanation of why the efficiency of the tiltrotor is low in cruise mode, and why a variable-diameter rotor is beneficial is here: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19970005490.pdf
| Free forum by Nabble | Edit this page |